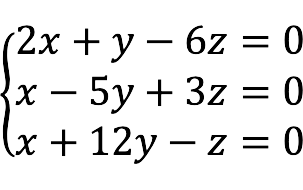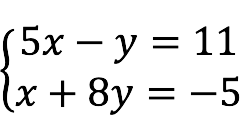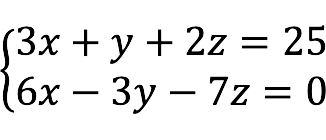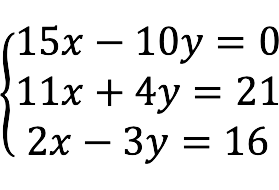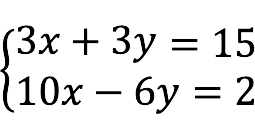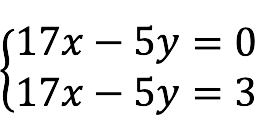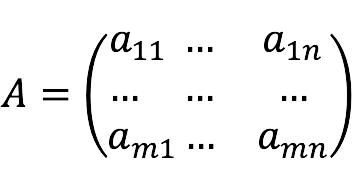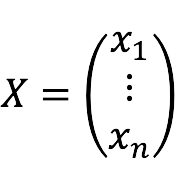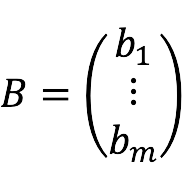Stelsel van lineaire algebraïsche vergelijkingen

In deze publicatie gaan we in op de definitie van een stelsel van lineaire algebraïsche vergelijkingen (SLAE), hoe het eruitziet, welke typen er zijn, en ook hoe het gepresenteerd kan worden in een matrixvorm, inclusief een uitgebreide.

Definitie van een stelsel lineaire vergelijkingen

Stelsel van lineaire algebraïsche vergelijkingen (of kortweg "SLAU") is een systeem dat er over het algemeen als volgt uitziet:

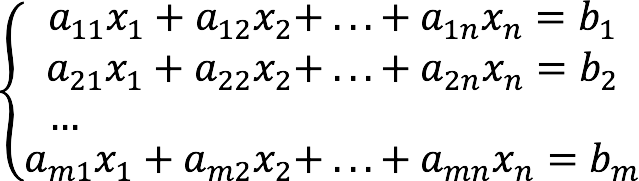
• m is het aantal vergelijkingen;
• n is het aantal variabelen.
• x₁, x₂,…, X_n - onbekend;
• a₁₁,₁₂…, A_mn – coëfficiënten voor onbekenden;
• b₁, b₂,…, B_m – gratis leden.

Coëfficiëntindices (a_ij) worden als volgt gevormd:

• i is het nummer van de lineaire vergelijking;
• j is het nummer van de variabele waarnaar de coëfficiënt verwijst.

SLAU-oplossing – zulke nummers c₁, C₂,…, C_n , in de setting waarvan in plaats van x₁, x₂,…, X_n, zullen alle vergelijkingen van het systeem in identiteiten veranderen.

Soorten SLAU

1. Homogeen – alle vrije leden van het systeem zijn gelijk aan nul (b₁ =b₂ = … = geb_m = 0).

   

2. Heterogeen – als aan bovenstaande voorwaarde niet wordt voldaan.
3. Square – het aantal vergelijkingen is gelijk aan het aantal onbekenden, dwz m = n.

   

4. onderbepaald – het aantal onbekenden is groter dan het aantal vergelijkingen.

   

5. overschreven Er zijn meer vergelijkingen dan variabelen.

   

Afhankelijk van het aantal oplossingen kan SLAE zijn:

1. Gezamenlijk tenminste één oplossing heeft. Bovendien, als het uniek is, wordt het systeem definitief genoemd, als er meerdere oplossingen zijn, wordt het onbepaald genoemd.

   

   Bovenstaande SLAE is gezamenlijk, want er is in ieder geval één oplossing: x = 2, y = 3.

2. onverenigbaar Het systeem heeft geen oplossingen.

   

   De rechterkant van de vergelijkingen is hetzelfde, maar de linkerkant niet. Er zijn dus geen oplossingen.

Matrixnotatie van het systeem

SLAE kan in matrixvorm worden weergegeven:

BIJL = B

• A is de matrix gevormd door de coëfficiënten van de onbekenden:

  

• X – kolom met variabelen:

  

• B – kolom met gratis leden:

  

Voorbeeld

We geven het onderstaande stelsel vergelijkingen weer in matrixvorm:

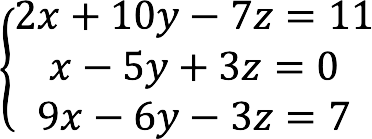
Met behulp van de bovenstaande formulieren stellen we de hoofdmatrix samen met coëfficiënten, kolommen met onbekende en vrije leden.

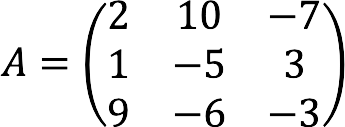
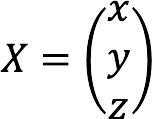
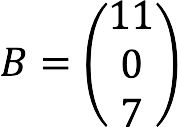
Volledig overzicht van het gegeven stelsel vergelijkingen in matrixvorm:

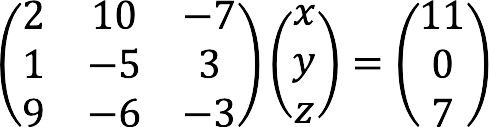
Uitgebreide SLAE-matrix

Als naar de matrix van het systeem A voeg gratis ledenkolom toe aan de rechterkant B, door de gegevens te scheiden met een verticale balk, krijg je een uitgebreide matrix van SLAE.

Voor het bovenstaande voorbeeld ziet het er als volgt uit:

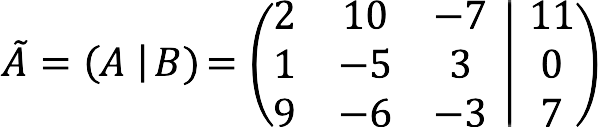
– aanduiding van de uitgebreide matrix.